
This callback is executed after a given event happened. By default it will listen out for all events, you can also listen out for specific events by passing event's name. The on_before callback is executed before a given event happens. Otherwise, all exit state changes will be watched. By passing state name you can narrow down the listener to only watch out for exit state changes.

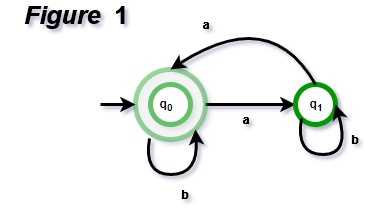
The on_exit callback is executed after a given state change happens. Otherwise, all transition state changes will be watched. By passing state name you can narrow down the listener to only watch out for transition state changes. The on_transition callback is executed when given state change happens. Otherwise, all enter state changes will be watched. By passing state name you can narrow down the listener to only watch out for enter state changes. The on_enter callback is executed before given state change is fired. This provides means for guaranteed initialization and cleanup. Note Regardless of how the state is entered or exited, all the associated callbacks will be executed. new do initial :red event :ready, :red => :yellow event :go, :yellow => :green event :stop, :green => :red on_before :ready do | event, time1, time2, time3| Use Myhill-Nerode theorem to show the following languages are not regular.Here is a very simple example of a state machine:įm = FiniteMachine. The output is 1 if the last three symbols read are in alphabetical order i.e., abc, bcd or cde. If they belong to different blocks, split this block into two or more blocks depending on the a-successors of the states.įor example, if a block has satisfying the following condition. Consider the a-successors of them for a ∊ Σ. Step 2. Consider the set of states in a block. (Any state in F is distinguishable from a state in K - F by ε.) Repeat the following step till no more split is possible. We get a partition of the set of states of K as follows: Then, xa and ya will belong to the same equivalence class of R L. Suppose x and y belong to the same equivalence class of R L. This definition is consistent as R L is right invariant. Let denote the equivalence class of R L to which x belongs.Ĭonstruct a DFSA M L = ( K′, Σ, δ′, q 0, F′) as follows: K′ contains one state corresponding to each equivalence class of R L. xR L y if ∀z in Σ*, xz is in L exactly when yz is in L or we can also write this in the following way: xR L y if for all w, z in Σ*, xwz is in L exactly when ywz is in L. Therefore, E is a refinement of R L and so the index of R L is less than or equal to the index of E and hence finite.įirst, we show R L is right invariant. Hence, any equivalence class of E is completely contained in an equivalence class of R L. Hence, xz and yz are both in L or both not in L as L is the union of some of the equivalence classes of E. xz and yz are in the same equivalence class of E. Let R L be defined as in the statement of the theorem. L is the union of those equivalence classes of R M which correspond to final states of M.Īssume statement (2) of the theorem and let E be the equivalence relation considered. It can be easily seen that this equivalence relation R M is right invariant, i.e., if (If a state is not reachable from q 0, it can be removed without affecting the language accepted). The number of equivalence classes is therefore equivalent to the number of states of M, assuming every state is reachable from q 0. The set of strings which take the machine from q 0 to a particular state q i are in one equivalence class. So R M divides Σ* into equivalence classes. R M is an equivalence relation, as seen below. Define a relation R M on Σ* such that xR My if δ( q 0, x) = δ(q 0, y). Let L be accepted by a FSA M = ( K, Σ, δ, q 0, F). Let equivalence relation R L be defined over Σ* as follows: xR L y if and only if, for all z ∊ Σ*, xz is in L exactly when yz is in L. L is the union of some of the equivalence classes of a right invariant equivalence relation of finite index on Σ*.


 0 kommentar(er)
0 kommentar(er)
